Evanescent Wave Analystical Tools
Silvia Mittler
These techniques are the fundament of the photonic work done in the group. The
evanescent fields of waveguide modes and surface plasmon resonances are used to
detect changes right within these fields. Therefore very often the sample of interest
is located on top of a waveguide or on top of a gold layer there where these evanescent
fields are present. Changes which can be detected by theses "films of light" are
typically optical changes: refractive index, absorption coefficients and thickness.
Any treatment of a material which changes one of the previously mentioned optical
qualities can therefore be also monitored. For example: Adsorption processes of
any kind to the waveguide surface or to the gold surface: both physisorption and
chemisorption processes, photo bleaching reactions, where the refractive index
of the material is changed, thermal expansion of material,......

A scheme of a planar waveguide carrying
a coupling grating is shown.
The refractive index of the waveguiding layer has to be higher than the refractive indices of the
surrounding materials to assure a total internal reflection and a guiding of the light within this particular film.
There are specific resonances where such a guiding takes place.
Having a close look to the field distribution of the electrical field in the resonance cases one finds a standing
wave across the structure with evanescent fields both located in the cladding and the substrate.
These resonances can be excited in two polarisation directions, denoted TE-modes for s-polarised light and TM-modes
for p-polarised light.
Therefore a probing of the waveguide film itself and of material located on top can be done out-of-plane and in-plane by choosing the
proper polarisation condition. Also each individual mode has its own propagation constant (beta) or effective refractive index N.
These numbers can be measured by measuring the resonant coupling angle theta for each mode and plug it into the equation for N.
Here one must know the periodicity of the coupling grating (capital lambda), the coupling order (m) and the wavelength of the
used light (small lambda).
By measuring more than one mode in both polarisation directions, it is possible to calculate the thickness and both refractive indices of
of an adlayer or the waveguide itself. Anisotropic changes can be monitored by this method as well.

In the case of a surface plasmon resonance not a guiding film is necessary, but
a metal-dielectric interface typically located on a substrate for handling purposes.
In this geometry only one resonance excists. Therefore one needs to know more
details about the system under consideration to measure specific quantities. Neverthless
the strength of the evanescent field in the case of a surface plasmon is larger
than for waveguide modes. Therefore the sensitivity is typically larger with surface
plasmon resonances in comparison to waveguide modes. Also a surafce plasmon is
a guided wave. It also has a propagation constant beta. The energy is not carried
very far, because the metal dissipates it in about one micrometer.

A combination of surface plasmons and waveguide modes is possible. This allows to independetly determine
the out-of-plane refractive index and the film thickness of material located on a metal.

Detail of the prism - gold sample geometry in Kretschmann configuration with
a cuvette for fluid sample handling.
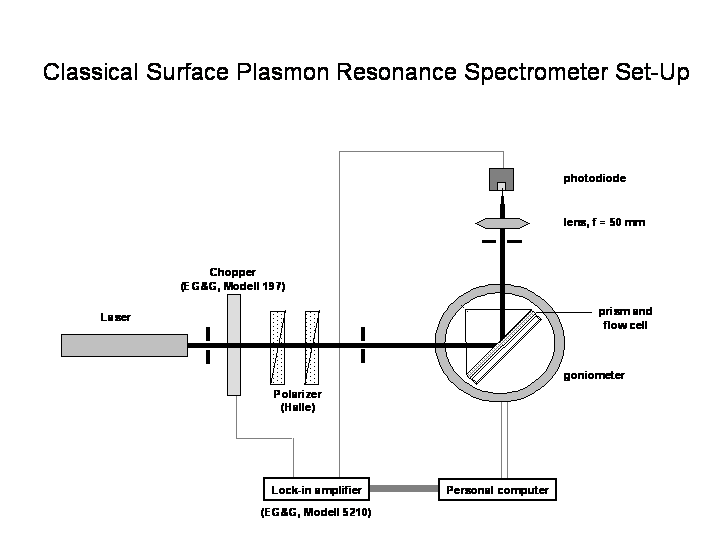
The entire set-up for surface plasmon resonance spectroscopy. Laser light in
p-polarisation attenuated to a defined intensity is incident on the prism-sample
mount. The prism-sample mount is located on a turning stage in order to change
the incident angle theta. The back refelcted light is collected via a lens and
a detector unit under two theta.
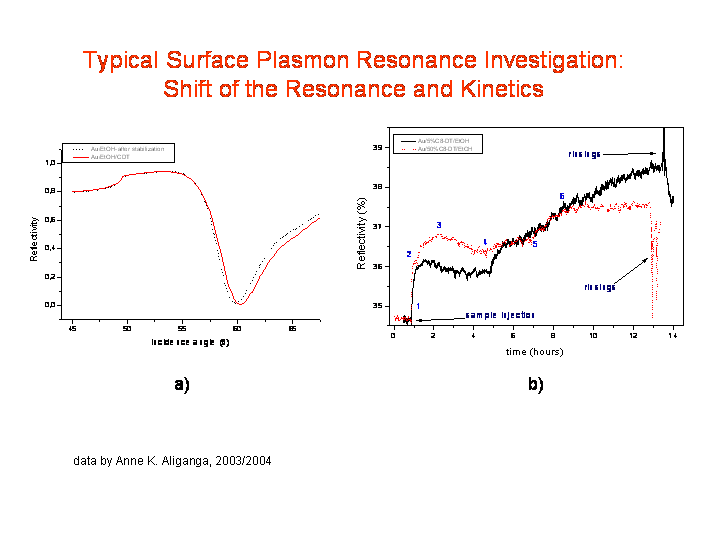
In figure a) a typical surface plasmon resonance curve is shown: the reflected
intensity versus the angle of incidence on the prism. The reflectivity starts
from a value below 1.0 and increase to a reflectivity close to 1 at the critical
angle of total internal reflection (here around 50 degree). Then the reflectivity
stays more or less constant and starts to decrease until a minimum value close
to zero is reached. With increasing angle of incidence the intensity recovers
in a slightly assymetric form. The entire depression in the reflectivity curve
is called surface plasmon. The resonance angle is located in the minimum. By
adding an ad-layer to the gold film the resonance of the surface plasmon shifts
to a higher angle of incidence due to the dispersion (red curve)..
In figure b) two kinetic experimenta are depicted. The experimental set-up
was fixed to an angle of incidence very close to the minimum, but on the left
side of it, where the surface plasmon resonace curve shows a nearly linear shape.
By adsorbing material to the gold the surface plasmon again shifts to the right,
but because of the fixed angle of incidence it yields an increase in reflected
intensity.

Typical waveguide set-up: the angle of incidence theta is scanned from left
to right across zero degree angle of incidence by a goniometer and monitoring
the out-coupled intensities, basically at both ends of the sample. Here just
one side is shown. In this particular example a bleaching beam is present, which
does a photo reactioin within the waveguide material. So by measuring the coupling
angles with increasing bleaching time the photo reaction can be monitored, because
it changes the optical constants of the waveguide.

a) Typical angle spectrum of a waveguide with one waveguide mode in each polarisation
direction. The waveguide modes were coupled by gratings into the structure and
are scanned individually roughly across zero degree angle of incidence. They
appear symmetrically around zero degree. Therefore the angle scale can be precisely
recalculated by the position of the peak-pairs. This allows drift free experiments.
b) The effective refractive index of the TM0 mode (p-polarisation) was calculated
out of data like shown in a) for various temperatures and plotted versus the
temperature. The TM0 waveguide mode shows a strongly linear behaviour in temperature
due to linear thermal expansion.

Waveguide mode spectrum development with bleaching time and the corresponding
dadta analysis of the refractive index and the film thickness of the bleached
waveguide material. The example here shows a material which shows an increase
in film thickness due to the photo reaction. This is due to an increase of space
needed on the molecular level. On the other hand with this volume incraese a
density decrease is occuring, which is represented in the decrease of the refractive
index. (data from Bernhard Menges and Alexander Theis)
Silvia
Mittler Home
April 2007
Department of Physics and
Astronomy , University of Western
Ontario
Comments to smittler@uwo.ca









